VFD PID Control: A Comprehensive Guide to Proportional-Integral-Derivative Control in Variable Frequency Drives
1. Introduction to PID Control
1.1 What is PID Control?
PID (Proportional-Integral-Derivative) control is a widely used feedback control algorithm in industrial automation systems. It is designed to maintain a process variable at a desired setpoint by calculating and applying a correction based on proportional, integral, and derivative terms.
Core Principle:
PID control continuously calculates an error value as the difference between a desired setpoint (SP) and a measured process variable (PV), then applies a correction based on three terms to minimize this error.
1.2 Importance of PID Control in Industrial Automation
PID control plays a crucial role in modern industrial automation for several reasons:
Precision Control:
- Maintains process variables at desired setpoints with high accuracy
- Reduces variations and deviations in production processes
- Improves product quality and consistency
Versatility:
- Suitable for a wide range of industrial applications
- Works with various types of sensors and actuators
- Adaptable to different process dynamics
Robustness:
- Performs well under varying load conditions
- Tolerates changes in system parameters
- Provides stable operation across different operating points
1.3 PID Control vs Other Control Methods
|
Control Method
|
Complexity
|
Precision
|
Tuning Difficulty
|
Application Suitability
|
|
PID Control
|
Medium
|
High
|
Medium
|
Most industrial processes
|
|
On-Off Control
|
Low
|
Low
|
None
|
Simple temperature control
|
|
Proportional Control
|
Low
|
Medium
|
Low
|
Simple level control
|
|
Fuzzy Logic Control
|
High
|
High
|
High
|
Complex nonlinear processes
|
|
Model Predictive Control
|
Very High
|
Very High
|
Very High
|
Advanced process control
|
2. PID Control Fundamentals
2.1 PID Controller Structure
A PID controller consists of three main components that work together to calculate the control output:
**
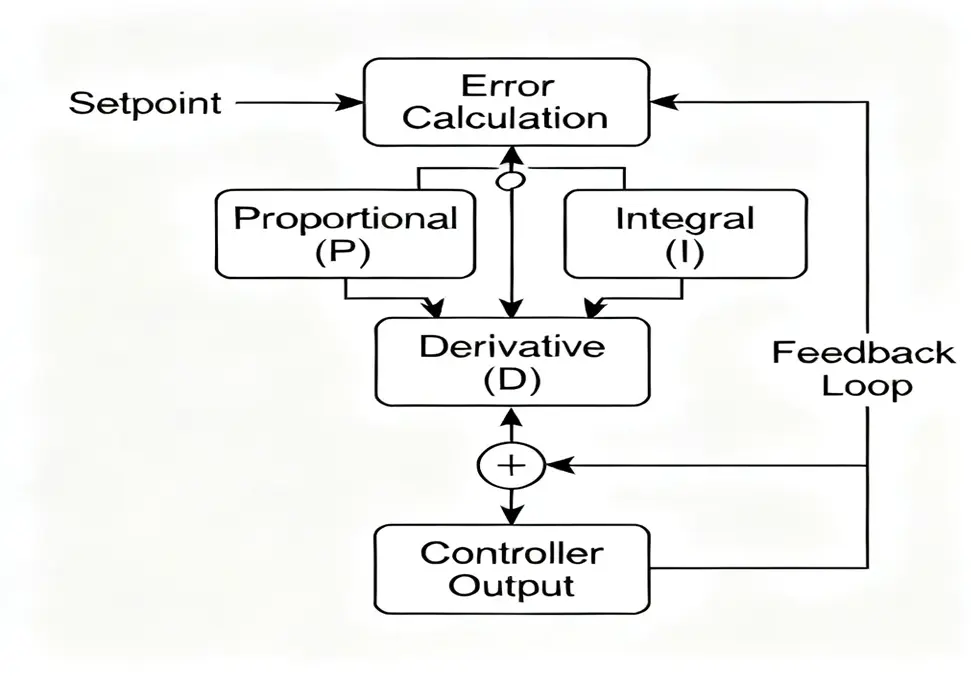
1. Proportional (P) Term
- Responds to the current error
- Output is proportional to the magnitude of the error
- Provides immediate correction action
2. Integral (I) Term
- Responds to the accumulated error over time
- Eliminates steady-state error
- Provides long-term correction
3. Derivative (D) Term
- Responds to the rate of change of the error
- Predicts future error trends
- Reduces overshoot and oscillation
2.2 Mathematical Formulation
The PID control algorithm can be expressed mathematically as:
Continuous-time PID equation:
u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt
Where:
- u(t) = Controller output
- Kp = Proportional gain
- Ki = Integral gain
- Kd = Derivative gain
- e(t) = Error = Setpoint – Process variable
- ∫e(t)dt = Integral of error over time
- de(t)/dt = Rate of change of error
Discrete-time PID equation (for digital implementation):
u(k) = Kp * e(k) + Ki * T * Σe(i) + Kd/T * [e(k) – e(k-1)]
Where:
- k = Current sample time
- T = Sampling period
- Σe(i) = Sum of errors from i=0 to k
- e(k-1) = Error at previous sample time
2.3 Understanding PID Terms
Proportional (P) Term Characteristics:
- Effect: Produces an output proportional to the current error
- Advantages: Fast response to changes in error
- Disadvantages: Creates steady-state error, may cause overshoot
Integral (I) Term Characteristics:
- Effect: Integrates the error over time and produces output based on accumulated error
- Advantages: Eliminates steady-state error
- Disadvantages: Slows down response, may cause instability if too large
Derivative (D) Term Characteristics:
- Effect: Produces output based on the rate of change of error
- Advantages: Reduces overshoot, improves stability
- Disadvantages: Sensitive to noise, no effect on steady-state error
2.4 PID Control Modes
P-Only Control:
- Uses only proportional term
- Simple but has steady-state error
- Suitable for simple applications with allowable error
PI Control:
- Combines proportional and integral terms
- Eliminates steady-state error
- Most commonly used in industrial applications
PD Control:
- Combines proportional and derivative terms
- Improves transient response
- Rarely used alone due to steady-state error
PID Control:
- Combines all three terms
- Provides best overall performance
- Most versatile but requires careful tuning
3. PID Control in Variable Frequency Drives
3.1 VFD PID Control System Overview
Variable Frequency Drives (VFDs) with built-in PID control functionality provide precise control of motor speed based on feedback from external sensors.
**
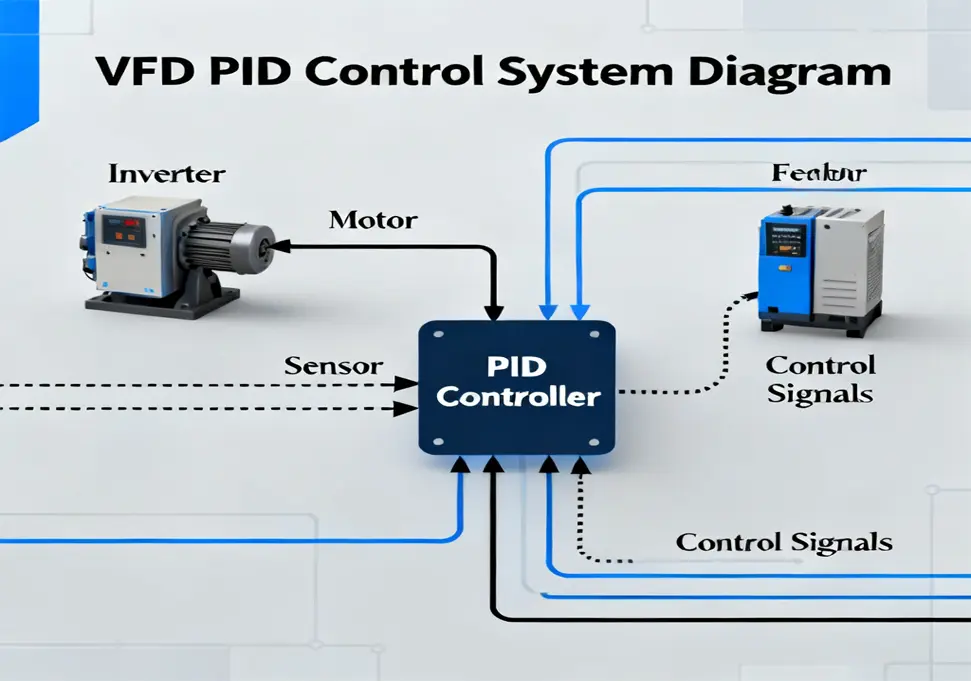
System Components:
- VFD with PID Controller: Main control unit
- Electric Motor: Controlled actuator
- Process Sensor: Measures the controlled variable
- Feedback Signal: Transmits sensor data to VFD
- User Interface: For parameter configuration and monitoring
3.2 How VFD PID Control Works
The PID control process in a VFD follows these steps:
1. Setpoint Configuration:
- User sets desired target value (e.g., pressure, flow, temperature)
- Setpoint can be fixed or dynamically adjusted
2. Feedback Acquisition:
- Sensor measures actual process variable
- Analog signal (4-20mA or 0-10V) sent to VFD’s analog input
3. Error Calculation:
- VFD computes error = Setpoint – Feedback value
- Error signal is processed by PID algorithm
4. PID Calculation:
- Proportional, integral, and derivative terms are computed
- Control output is determined based on PID parameters
5. Output Adjustment:
- VFD adjusts output frequency based on PID calculation
- Motor speed changes to correct the error
- Process variable moves toward setpoint
3.3 Benefits of VFD PID Control
Energy Efficiency:
- Motor runs only at required speed
- Reduces energy consumption compared to constant speed operation
- Eliminates mechanical throttling losses
Precision Control:
- Maintains process variables at exact setpoints
- Reduces process variations and improves quality
- Provides consistent operation under varying loads
Mechanical Protection:
- Smooth acceleration and deceleration
- Reduces mechanical stress on equipment
- Extends motor and machinery lifespan
Operational Flexibility:
- Easy adjustment of setpoints
- Adaptable to changing process requirements
- Remote control capability
3.4 VFD PID Control Applications
1. Pressure Control:
- Water supply systems
- Air compressors
- Hydraulic systems
- Steam systems
2. Flow Control:
- Pumping systems
- Fan systems
- Chemical processing
- Water treatment
3. Temperature Control:
- HVAC systems
- Ovens and furnaces
- Heat exchangers
- Cooling systems
4. Level Control:
- Tank level control
- Hopper level control
- Weighing systems
- Material handling
4. PID Parameter Configuration
4.1 Basic PID Parameters
Most VFDs with PID functionality allow configuration of the following basic parameters:
1. Proportional Gain (Kp)
- Function: Determines the sensitivity to current error
- Range: Typically 0.1 to 100.0
- Units: V/% or Hz/% depending on VFD manufacturer
2. Integral Time (Ti) or Integral Gain (Ki)
- Function: Determines the integral action strength
- Range: Ti: 0.1 to 1000 seconds; Ki: 0.001 to 10.0
- Relationship: Ki = Kp / Ti
3. Derivative Time (Td) or Derivative Gain (Kd)
- Function: Determines the derivative action strength
- Range: Td: 0 to 100 seconds; Kd: 0 to 100.0
- Relationship: Kd = Kp * Td
4.2 Advanced PID Parameters
1. Setpoint (SP)
- Target value for the controlled process variable
- Can be fixed or dynamically adjusted via analog input or communication
2. Feedback Selection
- Selection of analog input terminal for feedback signal
- Configuration of feedback signal type (4-20mA, 0-10V)
3. Output Limits
- Minimum and maximum output frequency
- Prevents the motor from operating outside safe limits
4. Integral Windup Protection
- Limits the integral term to prevent excessive output
- Resets integral term when output reaches limits
5. Derivative Filter
- Low-pass filter for derivative term
- Reduces sensitivity to noise in feedback signal
4.3 VFD-Specific PID Parameters
Different VFD manufacturers use different parameter numbering systems. Below are examples from major manufacturers:
Siemens MM440 VFD:
- P2200: PID mode selection
- P2253: Proportional gain Kp
- P2254: Integral time Ti
- P2255: Derivative time Td
- P2264: PID setpoint
- P2265: PID feedback selection
ABB ACS800 VFD:
- 9902: Application macro (select PID)
- 1201: PID proportional gain
- 1202: PID integral time
- 1203: PID derivative time
- 1205: PID reference (setpoint)
- 1206: PID feedback source
Schneider ATV312 VFD:
- P250: PID function activation
- P251: Proportional gain
- P252: Integral time
- P253: Derivative time
- P254: PID setpoint
- P255: Feedback input selection
4.4 Parameter Configuration Best Practices
1. Safety First:
- Set appropriate output limits to protect equipment
- Configure proper shutdown conditions
- Test with reduced gains initially
2. Signal Configuration:
- Ensure proper scaling of feedback signal
- Verify correct wiring of sensor
- Check for signal noise or interference
3. Initial Parameter Settings:
- Start with conservative values
- Disable integral and derivative terms initially
- Gradually increase gains while monitoring performance
4. Documentation:
- Record all parameter settings
- Document tuning process and results
- Save backup of working configuration
5. PID Parameter Tuning Methods
5.1 Manual Tuning (Trial and Error Method)
Manual tuning is the most common method for PID parameter adjustment, especially for simple systems.
**
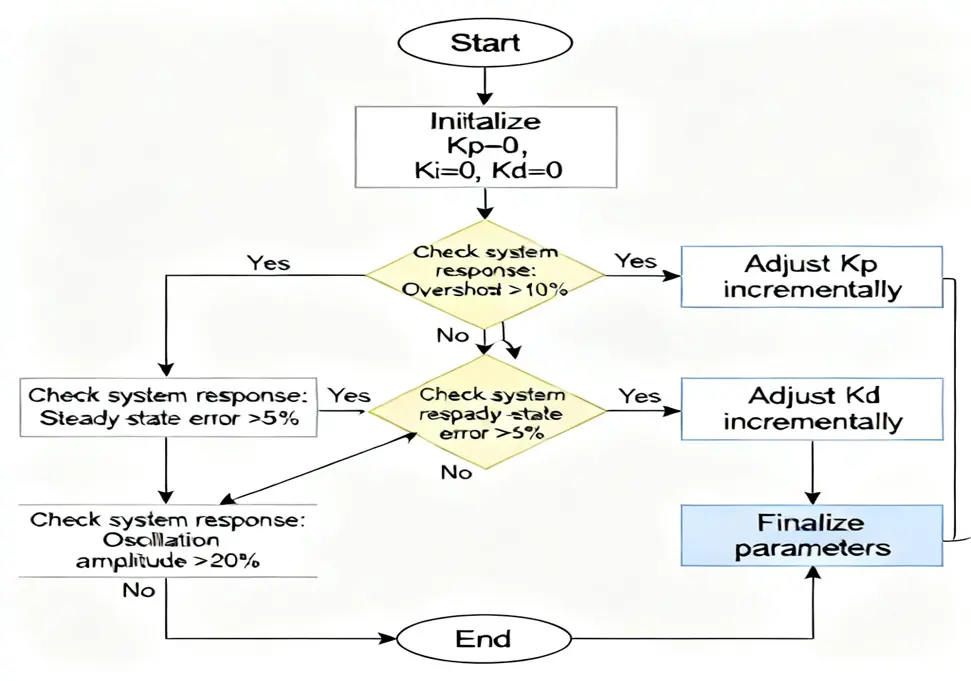
Step-by-Step Manual Tuning:
1. Initialization
- Set Ki = 0 and Kd = 0
- Set Kp to a small initial value (e.g., 0.1)
- Set output limits appropriately
2. Proportional Tuning
- Gradually increase Kp until the system starts to oscillate slightly
- Reduce Kp by 20-30% to stabilize the system
- Record this as the base proportional gain
3. Integral Tuning
- Set Ki to a small value (e.g., Kp/100)
- Gradually increase Ki until steady-state error is eliminated
- Stop when oscillation begins or response becomes too slow
4. Derivative Tuning
- Set Kd to a small value (e.g., Kp/10)
- Gradually increase Kd to reduce overshoot
- Stop when system becomes sensitive to noise
5. Fine Tuning
- Make small adjustments to all three parameters
- Optimize for fastest response with minimal overshoot
- Verify performance under different load conditions
5.2 Ziegler-Nichols Tuning Method
The Ziegler-Nichols method is a systematic approach based on the system’s dynamic response.
Ziegler-Nichols Closed-Loop Method:
1. Preparation
- Set Ki = 0 and Kd = 0
- Disable any integral or derivative actions
2. Determine Critical Gain (Kc)
- Gradually increase Kp until the system exhibits sustained oscillations
- Record the critical gain (Kc) where oscillations occur
- Measure the period of oscillation (Tc)
3. Calculate PID Parameters
|
Controller Type
|
Kp
|
Ti
|
Td
|
|
P
|
0.5Kc
|
–
|
–
|
|
PI
|
0.45Kc
|
0.83Tc
|
–
|
|
PID
|
0.6Kc
|
0.5Tc
|
0.125Tc
|
Ziegler-Nichols Open-Loop Method:
1. Step Response Test
- Apply a step change to the system
- Record the system’s response curve
- Determine delay time (L) and time constant (T)
2. Calculate PID Parameters
|
Controller Type
|
Kp
|
Ti
|
Td
|
|
P
|
1.2(T/L)
|
–
|
–
|
|
PI
|
0.9(T/L)
|
3.3L
|
–
|
|
PID
|
1.2(T/L)
|
2L
|
0.5L
|
5.3 Cohen-Coon Tuning Method
The Cohen-Coon method is another popular technique based on first-order plus dead time model.
Procedure:
- Perform a step response test
- Determine process gain (K), time constant (T), and dead time (τ)
- Calculate PID parameters using empirical formulas
Cohen-Coon Formulas for PID:
Kp = (1.35/T) * (T + τ/2)/(K * τ)
Ti = τ * (30 + 3(τ/T))/(9 + 20(τ/T))
Td = τ * 6/(2 + 3(τ/T))
5.4 Auto-Tuning Methods
Many modern VFDs include automatic tuning capabilities.
Auto-Tuning Process:
- Activate auto-tuning function on VFD
- VFD applies test signals to the system
- System response is measured and analyzed
- Optimal PID parameters are calculated automatically
- Parameters are applied to the controller
Advantages of Auto-Tuning:
- No manual intervention required
- Consistent results across similar systems
- Adaptable to changing system conditions
- Ideal for complex or hard-to-tune systems
Limitations of Auto-Tuning:
- May require system to be taken offline
- Test signals may disrupt normal operation
- Not always optimal for all operating conditions
- May need manual fine-tuning afterward
5.5 Tuning Guidelines for Specific Applications
Pressure Control:
- Kp: Medium to high (faster response needed)
- Ki: Medium (steady pressure important)
- Kd: Low to medium (prevent overshoot)
Flow Control:
- Kp: Medium (balance between response and stability)
- Ki: Medium to high (eliminate steady-state error)
- Kd: Low (flow tends to be noisy)
Temperature Control:
- Kp: Low to medium (process has large time constant)
- Ki: High (steady temperature critical)
- Kd: Medium to high (reduce overshoot)
Level Control:
- Kp: Low (prevent sloshing and overshoot)
- Ki: Medium (eliminate steady-state error)
- Kd: Very low or zero (level measurement noisy)
6. Practical Application Examples
6.1 Constant Pressure Water Supply System
System Description:
A typical constant pressure water supply system uses a VFD with PID control to maintain constant water pressure regardless of water demand.
Components:
- VFD with PID control
- Water pump motor
- Pressure sensor (4-20mA output)
- Pressure tank
- Pipeline system
Parameter Configuration:
|
Parameter
|
Value
|
Description
|
|
Setpoint (SP)
|
0.4 MPa
|
Desired water pressure
|
|
Feedback Input
|
AI1 (4-20mA)
|
Pressure sensor signal
|
|
Kp
|
5.0
|
Proportional gain
|
|
Ti
|
60 seconds
|
Integral time
|
|
Td
|
5 seconds
|
Derivative time
|
|
Min Frequency
|
25 Hz
|
Minimum pump speed
|
|
Max Frequency
|
50 Hz
|
Maximum pump speed
|
Control Process:
- Pressure sensor measures actual water pressure
- VFD compares measured pressure with setpoint (0.4 MPa)
- PID algorithm calculates required frequency adjustment
- VFD adjusts pump speed to maintain constant pressure
- When demand increases, pressure drops, VFD increases frequency
- When demand decreases, pressure rises, VFD decreases frequency
Expected Performance:
- Pressure stability: ±0.02 MPa
- Response time: <5 seconds
- Energy savings: 25-40% compared to fixed speed operation
6.2 Central Air Conditioning System
System Description:
A central air conditioning system uses VFD PID control to maintain constant room temperature by adjusting fan speed.
Components:
- VFD with PID control
- HVAC fan motor
- Temperature sensor (0-10V output)
- Duct system
- Air handler unit
Parameter Configuration:
|
Parameter
|
Value
|
Description
|
|
Setpoint (SP)
|
25°C
|
Desired room temperature
|
|
Feedback Input
|
AI2 (0-10V)
|
Temperature sensor signal
|
|
Kp
|
3.0
|
Proportional gain
|
|
Ti
|
120 seconds
|
Integral time
|
|
Td
|
10 seconds
|
Derivative time
|
|
Min Frequency
|
30 Hz
|
Minimum fan speed
|
|
Max Frequency
|
50 Hz
|
Maximum fan speed
|
Control Process:
- Temperature sensor measures room temperature
- VFD compares actual temperature with setpoint (25°C)
- PID controller calculates required fan speed adjustment
- VFD adjusts fan speed to maintain constant temperature
- When temperature rises above setpoint, fan speed increases
- When temperature drops below setpoint, fan speed decreases
Expected Performance:
- Temperature stability: ±0.5°C
- Energy savings: 30-50% compared to fixed speed
- Improved comfort with reduced temperature fluctuations
6.3 Conveyor Speed Synchronization
System Description:
Multiple conveyors in a production line need to be synchronized to prevent product jamming or spacing issues.
Components:
- Master VFD with PID control
- Slave VFDs with speed control
- Speed sensors (encoders)
- Conveyor motors
- Production line control system
Parameter Configuration:
|
Parameter
|
Value
|
Description
|
|
Setpoint Source
|
Master encoder
|
Speed reference from master conveyor
|
|
Feedback Source
|
Slave encoder
|
Actual speed of slave conveyor
|
|
Kp
|
8.0
|
Proportional gain
|
|
Ti
|
30 seconds
|
Integral time
|
|
Td
|
2 seconds
|
Derivative time
|
|
Speed Ratio
|
1.0
|
Speed ratio between master and slave
|
|
Max Speed Error
|
2%
|
Maximum allowable speed deviation
|
Control Process:
- Master conveyor runs at reference speed
- Slave conveyor speed is measured by encoder
- PID controller compares slave speed with master speed
- VFD adjusts slave motor speed to match master speed
- System maintains precise speed synchronization
- Any speed deviation is quickly corrected
Expected Performance:
- Speed synchronization accuracy: ±1%
- Response time to speed changes: <1 second
- Smooth product transfer between conveyors
6.4 Industrial Oven Temperature Control
System Description:
An industrial oven requires precise temperature control to ensure product quality and consistency.
Components:
- VFD with PID control
- Blower fan motor
- Temperature sensors (RTD or thermocouple)
- Heating elements
- Oven control system
Parameter Configuration:
|
Parameter
|
Value
|
Description
|
|
Setpoint (SP)
|
200°C
|
Desired oven temperature
|
|
Feedback Input
|
AI1 (RTD input)
|
Temperature sensor signal
|
|
Kp
|
2.0
|
Proportional gain
|
|
Ti
|
180 seconds
|
Integral time
|
|
Td
|
30 seconds
|
Derivative time
|
|
Min Frequency
|
20 Hz
|
Minimum fan speed
|
|
Max Frequency
|
50 Hz
|
Maximum fan speed
|
Control Process:
- Temperature sensors monitor oven temperature
- VFD compares actual temperature with setpoint (200°C)
- PID controller calculates required fan speed adjustment
- VFD adjusts blower speed to maintain uniform temperature
- Faster fan speed improves heat distribution
- Slower fan speed reduces energy consumption
Expected Performance:
- Temperature uniformity: ±2°C across oven chamber
- Setpoint accuracy: ±1°C
- Energy efficiency: Improved heat transfer reduces energy usage
7. Troubleshooting PID Control Systems
7.1 Common PID Control Problems
1. System Oscillation
Symptoms:
- Continuous oscillation around setpoint
- Increasing amplitude oscillations
- Unstable process variable
Possible Causes:
- Kp or Ki too large
- Td too small
- System resonance
- Sensor noise
Solutions:
- Reduce proportional gain (Kp)
- Increase derivative gain (Kd)
- Reduce integral gain (Ki)
- Add filtering to feedback signal
- Check for mechanical resonance
2. Slow Response
Symptoms:
- Process variable changes slowly
- Long time to reach setpoint
- Sluggish reaction to disturbances
Possible Causes:
- Kp too small
- Ki too small
- Td too large
- Output limits too tight
Solutions:
- Increase proportional gain (Kp)
- Increase integral gain (Ki)
- Reduce derivative gain (Kd)
- Adjust output limits
- Check for mechanical friction or binding
3. Steady-State Error
Symptoms:
- Process variable stabilizes but not at setpoint
- Persistent offset from desired value
- Integral term not eliminating error
Possible Causes:
- Ki too small
- Integral windup protection too aggressive
- Output limits preventing integral action
- Incorrect sensor calibration
Solutions:
- Increase integral gain (Ki)
- Adjust integral windup settings
- Check output limits
- Recalibrate sensor
- Verify setpoint configuration
4. Overshoot
Symptoms:
- Process variable exceeds setpoint
- Large overshoot followed by slow recovery
- Potential safety concerns
Possible Causes:
- Kp too large
- Ki too large
- Td too small
- System inertia
Solutions:
- Reduce proportional gain (Kp)
- Reduce integral gain (Ki)
- Increase derivative gain (Kd)
- Add feedforward control
- Implement anti-overshoot algorithms
5. Noise Sensitivity
Symptoms:
- Erratic output
- Rapid fluctuations around setpoint
- Unstable operation
Possible Causes:
- Kd too large
- Sensor noise
- Poor electrical grounding
- Signal interference
Solutions:
- Reduce derivative gain (Kd)
- Add low-pass filter to feedback
- Improve sensor wiring and shielding
- Check electrical grounding
- Move sensor away from interference sources
7.2 Systematic Troubleshooting Approach
Step 1: Verify System Basics
- Check power supply and wiring
- Verify sensor calibration
- Confirm VFD is in PID mode
- Check parameter settings
Step 2: Analyze System Response
- Apply step change to setpoint
- Record system response curve
- Identify specific problem (oscillation, overshoot, etc.)
- Compare with desired performance
Step 3: Check Feedback Signal
- Monitor feedback signal with oscilloscope
- Look for noise or interference
- Verify proper scaling and offset
- Check sensor mounting and alignment
Step 4: Adjust PID Parameters
- Make incremental changes to one parameter at a time
- Allow system to stabilize after each change
- Document changes and results
- Follow tuning guidelines for specific application
Step 5: Test Under Different Conditions
- Test at different setpoints
- Verify performance under varying loads
- Check response to disturbances
- Confirm stability over extended periods
7.3 Preventive Maintenance
Regular Maintenance Tasks:
1. Sensor Maintenance
- Clean sensor regularly
- Check sensor calibration
- Verify sensor mounting and alignment
- Replace worn or damaged sensors
2. Electrical System Check
- Inspect wiring for damage or corrosion
- Check electrical connections for tightness
- Verify grounding integrity
- Test for electrical noise or interference
3. Parameter Backup
- Save current parameter settings
- Document any changes made
- Create backup of working configuration
- Compare current settings with baseline
4. Performance Monitoring
- Record system response data
- Track energy consumption
- Monitor wear on mechanical components
- Schedule maintenance based on usage
5. Training and Documentation
- Train operators on proper system operation
- Document troubleshooting procedures
- Maintain up-to-date system documentation
- Share best practices with maintenance team
7.4 Advanced Troubleshooting Techniques
1. System Identification
- Perform frequency response tests
- Develop mathematical model of system
- Use model to predict optimal PID parameters
- Validate model with actual system response
2. Data Logging and Analysis
- Log PID variables over time
- Analyze trends and patterns
- Identify correlation between parameters and performance
- Use statistical methods to optimize parameters
3. Simulation Tools
- Use simulation software to test PID parameters
- Model system dynamics and control algorithms
- Test different tuning methods virtually
- Validate changes before implementing on actual system
4. Expert Systems
- Implement rule-based expert systems
- Use machine learning to optimize PID parameters
- Develop adaptive control algorithms
- Implement self-tuning and self-optimizing systems
Summary
PID control is a powerful and versatile technique that plays a critical role in modern industrial automation, particularly in variable frequency drive applications. By understanding the fundamental principles of PID control and mastering the art of parameter tuning, engineers and technicians can achieve precise control of motor speed and process variables.
Key Takeaways:
- PID Fundamentals: The proportional, integral, and derivative terms each play distinct roles in the control process, and their proper balance is essential for optimal performance.
- VFD Integration: Modern VFDs with built-in PID functionality provide a cost-effective solution for precise motor speed control based on process feedback.
- Parameter Tuning: Successful PID control requires careful parameter tuning using methods like manual adjustment, Ziegler-Nichols, or automatic tuning algorithms.
- Application-Specific Considerations: Different applications (pressure control, temperature control, etc.) require different PID parameter settings and tuning approaches.
- Troubleshooting Skills: Systematic troubleshooting and preventive maintenance are essential for maintaining reliable PID control system performance.
- Advanced Techniques: System identification, data analysis, and simulation tools can help optimize PID control performance for complex applications.
By applying the knowledge and techniques presented in this guide, professionals can design, implement, and maintain effective PID control systems that improve process efficiency, reduce energy consumption, and enhance product quality in industrial applications.

